Optimal Deployment of Wireless Sensor Nodes using Particle Swarm Optimization (PSO), Ant Colony Optimization (ACO)

Abstract

Wireless Sensor Networks (WSNs) are emerging as a significant area of research due to their potential to autonomously monitor physical and environmental conditions. These networks comprise spatially distributed, low-cost sensor nodes with limited transmission range, processing capabilities, storage, and energy resources. The primary function of these networks is to collect data from various nodes and transmit it to a base station for subsequent processing. WSNs present several challenges, including optimal sensor deployment, node localization, base station placement, target node location, energy-aware clustering, and data aggregation. Recently, global researchers have been employing a bio-inspired optimization algorithm, Particle Swarm Optimization (PSO), to enhance the efficiency of WSNs. This report explores the application of the PSO algorithm for optimal sensor deployment in WSNs, contributing to the ongoing efforts to maximize the potential of these networks.

Introduction

I. INTRODUCTION

In the rapidly evolving world of wireless sensor networks (WSNs), the strategic placement of sensor nodes is paramount. It plays a pivotal role in enhancing network performance and optimizing resource utilization. This report aims to delve into the complexities of optimizing the deployment of wireless sensor nodes, with a particular focus on two advanced algorithms - Particle Swarm Optimization (PSO) and Ant Colony Optimization (ACO).

WSNs are characterized by their distributed nature and inherent resource constraints. These characteristics necessitate the development of efficient strategies for node placement. The goal is to ensure comprehensive coverage, maximize energy efficiency, and facilitate robust data collection. In this context, PSO and ACO emerge as promising solutions.

PSO, an algorithm inspired by social behavior and natural phenomena, and ACO, which models the foraging behavior of ants, have been recognized for their effectiveness in addressing complex optimization challenges. These challenges are inherent in the deployment of WSNs. These algorithms iteratively refine node positions by leveraging the collective intelligence of nodes or agents. The objective is to strive toward an optimal solution that balances coverage, connectivity, and energy consumption.

This report provides a comprehensive exploration of PSO and ACO methodologies. It aims to elucidate their theoretical underpinnings, delve into the intricacies of their algorithms, and highlight their practical implications in the context of WSN deployment optimization. The report will also present empirical evaluations and comparative analyses. These will assess the efficacy and suitability of PSO and ACO in various deployment scenarios, shedding light on their strengths, limitations, and potential avenues for further research.

II. PARTICLE SWARM OPTIMIZATION

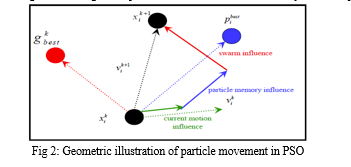
Particle Swarm Optimization (PSO), conceptualized by Eberhart and Kennedy in 1995, stands as a population-based optimization technique. In this method, particles, representing potential solutions, traverse the problem space by mimicking the movement of the current optimum particles. Each particle maintains its coordinates in the problem space along with the best solution (fitness) it has attained thus far, termed as pbest. Additionally, PSO tracks another crucial metric: the best value achieved by any particle in the swarm, denoted as gbest. Each particle dynamically adjusts its velocity based on its individual flying experience (pbest) and the collective experience of the swarm (gbest), aiming to guide the population towards more favorable solution regions. Operating within a D-dimensional search space, each particle is akin to a volume-less entity. The manipulation of particles follows a set of equations, orchestrating their movement towards optimal solutions.

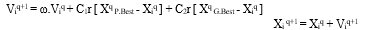
The first part of the equation is the previous velocity of the particle. The second is the “cognition” part, representing the exploiting of its own experience, where c1 is an individual factor. And the third is the “social” pan. representing the shared information and cooperation among the particles, where c2 is the societal factor.

A. PSO Parameters

For the proposed method the number of particles is taken as 10 and the learning factor C1= C2= 2. An inertia weight factor is linearly reduced as the search proceeds from 0.9 to 0.4. The maximum velocity and maximum iterations are taken as 50 and 300 respectively.

B. Performance Improvement

Particle Swarm Optimization (PSO) is known for its quick convergence and consistent efficiency, regardless of the complexity of the problem space, such as the number of peaks and dimensions. However, it does face certain challenges, including premature convergence and sensitivity to parameter settings, which can lead to local rather than global optimization. As a result, a significant amount of research has been dedicated to overcoming these obstacles. Strategies include adapting parameters, enhancing diversity, and modifying the algorithm to strengthen PSO’s global optimization abilities and facilitate dynamic adaptation.

C. Optimal WSN Deployment

The Wireless Sensor Network (WSN) conundrum revolves around determining the strategic placement of sensor nodes to achieve desired coverage, connectivity, and energy efficiency while minimizing node count. Inadequate sensor coverage results in unnoticed events, while dense sensor populations lead to congestion and delays. Optimal WSN deployment ensures quality of service, prolonged network lifespan, and cost-effectiveness. Existing PSO solutions for deployment are typically computed centrally, often on a base station, to ascertain sensor positions.

D. Sensor Coverage

A sensor positioned at coordinates (X1, Y1) effectively covers another point (X2, Y2) if the Euclidean distance between them satisfies the condition: (X1-X2)2 + (Y1-Y2)2 ≤ r2, where r represents the sensor's sensing range. The mean value of location points (Xi, Yi) for i=1, 2, ..., M is denoted as (mx, my). The sensor node serves as the centroid of the location points it covers, with the sensing range r determined by the distance between the sensor node and the farthest location point. Area A is partitioned into R regions, each allocated sensor node by minimizing the Euclidean distance between location points and their respective centroids. Consequently, Area A is covered by R sensor nodes. Formulating the coverage problem as an optimization task involves determining the optimal deployment of R sensors across the set of points P, ensuring comprehensive coverage of every location point.

E. Problem Formulation

The primary aim of this study is to optimize the deployment of sensor nodes in a network. The goal is to minimize the distance between adjacent nodes, thereby maximizing network coverage, while concurrently adhering to all constraints.

The following assumptions underpin this study:

1. All sensor nodes are identical and possess mobility.
2. It is assumed that the deployed sensor nodes can comprehensively cover the sensing fields. Both the sensing coverage and communication coverage of each node are presumed to be circular, devoid of any irregularities.
3. The design variables in this study are the two-dimensional coordinates of the sensor nodes.
4. Each sensor node is assumed to cover an equal area of the sensing field.

These assumptions are commonly made in numerous sensor network applications and form the basis of our analysis in this report.

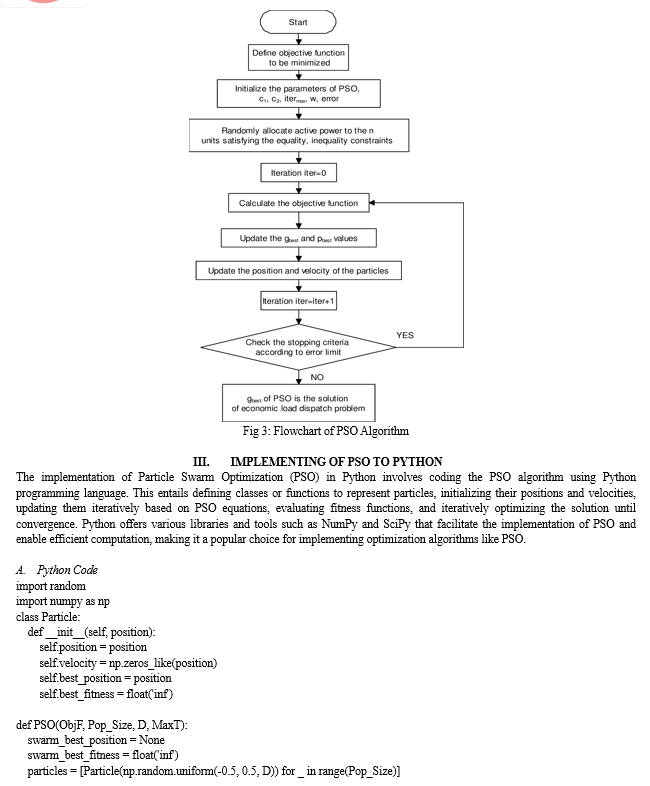
F. Flow Chart

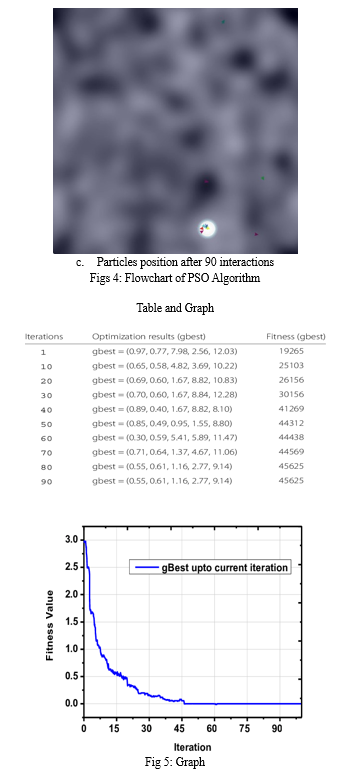
In the context of wireless sensor networks, the concept of fitness, denoted as (F), is determined by the Euclidean distance between a sensor node and its nearest centroid. The calculation of fitness for each particle involves evaluating its proximity to the optimal solution. The particle within the swarm that exhibits the lowest fitness is identified as the global best particle, indicating its closeness to the optimal solution. The achievement of the swarm is recognized when all particles attain fitness values that are less than or equal to the range of the sensor network.

The Particle Swarm Optimization (PSO) process can be outlined as follows:

1. Initialization: The network information and algorithm parameters, including inertia, weight, learning factor, velocity boundary value, and maximum iteration count, are initialized. An array of particles is also initialized with random position and velocity vectors.
2. Fitness Calculation: The fitness for each particle at its current position is calculated by determining the distance to its nearest sensor.
3. Fitness Minimization: The fitness values are minimized with the ideal goal of reaching zero, indicating that the distance between points of interest and their nearest sensors falls within the sensor’s sensing range. If a particle’s fitness surpasses the current best, it is designated as the best particle for the subsequent move, and its fitness is updated accordingly.
4. Position and Velocity Adjustment: Each particle’s position and velocity are adjusted based on the calculated fitness.
5. Position Evaluation: The algorithm determines whether the next position of the particle yields an improvement; if so, the particle adopts the new position, otherwise, the algorithm continues with the existing position.
6. Iterative Process: The process is repeated iteratively until all particles communicate with each other, collectively maximizing coverage.

This iterative process propels the optimization of sensor node deployment within the network, aiming towards comprehensive coverage and efficient resource utilization. This professional exploration of PSO provides a robust framework for optimizing wireless sensor networks, contributing to the advancement of this dynamic field.

V. ANT COLONY OPTIMIZATION

A. Introduction

Ant Colony Optimization (ACO) emerged in the 1990s as a pioneering metaheuristic algorithm inspired by the foraging behavior of ants. It was conceptualized by Marco Dorigo and his team, drawing insights from observations of ant colonies' efficient food-gathering processes. ACO falls within the domain of swarm intelligence, leveraging the collective actions of simple agents to address complex optimization problems. Historically, Marco Dorigo, during his tenure at the Free University of Brussels, developed the foundational Ant System, an early instance of ACO tailored for solving the Traveling Salesman Problem (TSP). Since its inception, ACO has undergone substantial refinement, leading to its widespread adoption across diverse optimization domains.

At its essence, ACO mimics ants' pheromone trail-laying behavior. Ants deposit pheromones along paths they traverse, with the intensity of these trails reflecting path attractiveness. The algorithm iteratively constructs solutions by probabilistically selecting components based on both pheromone trails and heuristic information. As iterations progress, paths yielding superior solutions accumulate more pheromones, steering subsequent iterations towards increasingly optimal solutions.

B. Key Components of ACO

1. Pheromone Trails: Representing collective memory guiding exploration.
2. Heuristic Information: Directing the search towards promising regions of the solution space.
3. Pheromone Update Rule: Governing pheromone deposition and evaporation, balancing between exploration and exploitation.

ACO has found application in diverse optimization challenges such as routing, scheduling, and logistics. Its efficacy in handling complex, combinatorial problems with irregular structures has made it indispensable in both academic research and industrial applications. The success of ACO has spurred further innovation, leading to the development of hybrid and variant algorithms tailored to address specific optimization challenges.

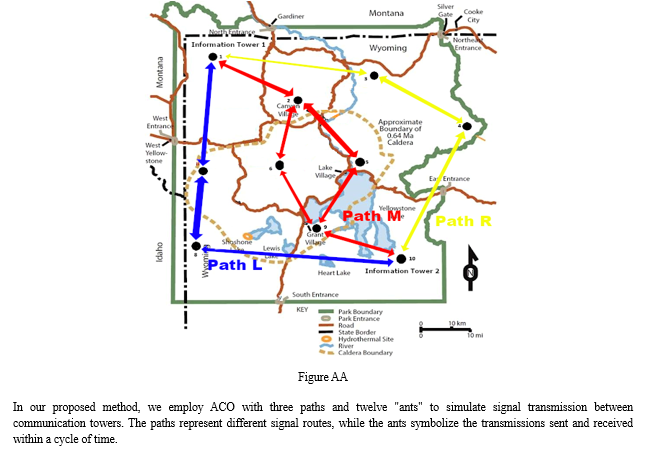
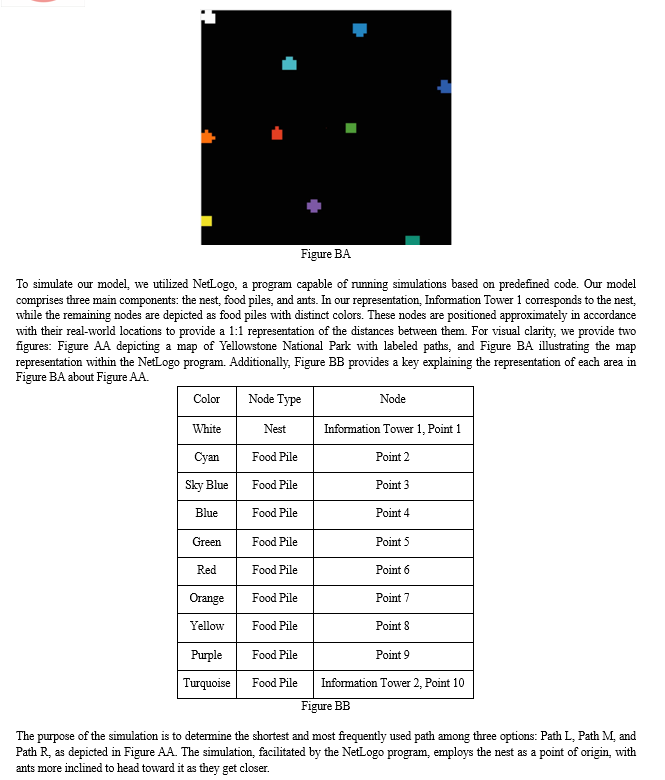
Conclusion

In conclusion, after a comprehensive analysis of Particle Swarm Optimization (PSO) and Ant Colony Optimization (ACO) for the crucial task of detecting wildfires using wireless sensor nodes in Yellowstone National Park, it becomes evident that PSO emerges as the superior choice. PSO showcases remarkable efficacy in optimizing the deployment of sensor nodes, efficiently maximizing the coverage area while minimizing energy consumption. Its ability to swiftly converge to optimal solutions, adapt to dynamic environmental changes, and mitigate the impact of local optima sets it apart in the context of wildfire detection. While ACO demonstrates notable capabilities, particularly in complex routing scenarios, its performance in this specific application falls short compared to PSO. The inherent characteristics of PSO, such as its simplicity, scalability, and robustness, make it the preferred optimization algorithm for ensuring timely and accurate wildfire detection, thereby significantly enhancing the safety and conservation efforts within Yellowstone National Park.

References

[1] J. Yick, B.Mukherjee, and D.Ghosal, “Wireless Sensor Network Survey”, computer networks, Vol 52,no-12,pp. 2292 2330,2008 [2] Eberhart R. and Kennedy J. (1995). A new optimizer using Particle Swarm Theory. Proc 6th Int. symposium on Micromachine and Human Science, pp.39-43 [3] Poli, R. 2007. Analysis of the publications on the Applications of Particle Swarm Optimisation, Journal of Artificial Evolution and Applications, 2008, 1-10. [4] Lazinica, A. 2009. Particle Swarm Optimization. (Edited), Published by In-Tech, Croatia, January [5] K.V. Price, R.M Storn, and J.A Lampinen, Differential evolution: A Practical Approach to Global Optimization, Ser. Natural Computing series; Berlin, Germany: Springer-Verlag, 2005

Copyright

Copyright © 2024 Kiruthikeswaran Rajaram. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.